Proposition 26.
If two triangles have two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, or that opposite one of the equal angles, then the remaining sides equal the remaining sides and the remaining angle equals the remaining angle.
두 각이 각각 같고 한 변이 같은 두 삼각형은(서로 같은 변이 두 각과 모두 만나거나 건너편에 있는 변이라도) 나머지 각과 변도 서로 같다.
보통 교과서에 한 변과 양 끝각이 같다고 적지만 굳이 양 끝각일 필요는 없음을 금세 알 수 있다. 삼각형의 내각의 합은 180도로 일정하다는 명제를 증명하지 않았기 때문에 이 명제는 둘로 나누어 증명한다.
$\triangle{ABC},\triangle{ DEF}$이 있다.
$$\angle{ABC}=\angle{DEF} ,\angle{BCA}=\angle{EFD}\tag{1}$$라고 하자.
먼저 1. $\overline{BC}=\overline{EF}$라 하고 나머지 두 변과 각이 서로 같음을 보이자. (한 변과 양 끝각이 같은 경우)
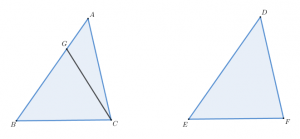
즉, $\overline{AB}=\overline{DE}$와 $\overline{AC}=\overline{DF}$이고 $\angle {BAC}=\angle {EDF}$ 임을 보이기로 하자.
만약에 $\overline{AB}\not=\overline{DE}$이면 어느 하나가 클 것이다.
이때, $\overline{AB}>\overline{DE}$라고 하면 $\overline{BG}=\overline{DE}$인 점 $G$를 잡을 수 있다.
$\overline{BG}=\overline{DE}$, $\overline{BC}=\overline{EF}$, $\angle{ABC}=\angle{DEF}$이므로 명제 4에 따라서
$$\triangle GBC\equiv\triangle DEF$$
$$\angle{GCB}=\angle{DFE}$$
이것은
$$\angle{GCB}=\angle{ACB}\;\;\;(\because (1)\angle{BCA}=\angle{EFD})$$라야 하므로 모순이다.
$$\therefore \overline{AB}=\overline{DE}$$
명제 4에 따라
$$\triangle ABC\equiv\triangle DEF$$
2. 다음으로 $\overline{AB}=\overline{DE}$이고 $\overline{BC}\not=\overline{EF}$라고 하자.
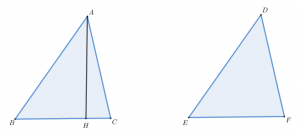
만약에 $\overline{BC}\not=\overline{EF}$이면 어느 하나가 클 것이다.
이때, $\overline{BC}>\overline{EF}$라고 하면 $\overline{BH}=\overline{EF}$인 점 $H$를 잡을 수 있다.
위와 마찬가지로
$$\triangle ABH\equiv\triangle DEF$$ 이므로
$$\angle BHA=\angle EFD$$이다.
이것은
$$\angle BHA=\angle BCA\;\;\;(\because (1)\angle{BCA}=\angle{EFD})$$가 되므로 모순이다.
따라서 $\overline{BC}=\overline{EF}$이므로
$$\triangle ABC\equiv\triangle DEF$$
$\blacksquare$
이처럼 그냥 외우면 간단한 정리도 막상 증명하려고 하면 상당한 공을 들여야 한다. 오죽하면 뛰어난 수학자 데카르트도 이 과정이 힘들어서 해석기하학을 만들었을까?
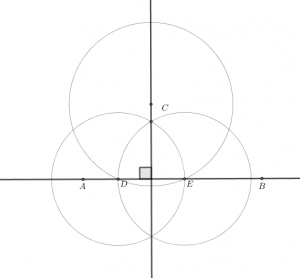
 두 각 $\angle CBE$와 $\angle EBD$의 합은 2직각이다.
두 각 $\angle CBE$와 $\angle EBD$의 합은 2직각이다.
 $\blacksquare$
$\blacksquare$