If two triangles have two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, then they also have the base equal to the base, the triangle equals the triangle, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides.
두 삼각형에서 두변과 사이에 낀 각이 서로 같다면 나머지 변과 각들은 서로 같다.
너무 당연해서 어떻게 증명해야 할까 고민된다. 먼저 ‘같다’는 어떻게 정의했을까 알아야 한다. 유클리드는 서로 포개서 꼭 맞게 겹쳐지는 것을 ‘같다’고 정의했다. 따라서 삼각형이 꼭 맞게 겹쳐짐을 보이면 된다.
아래 그림에서 변$AB$, 변$AC$가 변$DE$, 변$DF$와 각각 같고 각 $BAC$와 각$EDF$가 서로 같다고 가정하자.
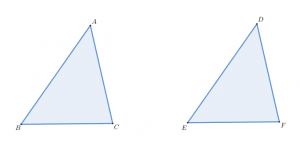
이제 나머지 변$BC$와 변$EF$, 각$ABC$는 각$DEF$와 같고 각$ACB$는 각$DFE$와 같음을 보이면 된다.
먼저 꼭짓점 $A$를 $D$에 포개어 놓고 직선 $AB$를 직선 $DE$에 포개어 놓자.
$\overline{AB}=\overline{DE}$이므로 꼭짓점 $B$는 $E$와 포개어 진다.
$\angle{ BAC}=\angle{EDF}$이므로 $AB$와 $DE$가 포개져 있으면 직선 $AC$와 직선 $DF$도 포개어 진다’.
따라서 점 $C$와 점 $F$도 포개진다. ($\because \overline{ AC }=\overline{DF}$)
앞에서 점 $B$와 점 $E$가 일치하므로 밑변 $BC$와 밑변 $EF$는 같다. (두 점을 잇는 선분은 단 하나다. )
그러므로 삼각형 $ABC$와 삼각형 $DEF$은 빈틈없이 포개어 진다.
그러므로 나머지 각도 서로 같다.
$$\angle {ABC}=\angle {DEF},\;\;\angle {ACB}=\angle {DFE}$$
$\blacksquare$
이렇게 두 삼각형이 같은 것을 합동($\equiv$)이라고 하고 기호로 아래처럼 적는다. 유클리드는 ‘합동’을 정의하지 않고 포개어 꼭 맞게 겹쳐짐을 보였다. 오늘날은 SAS(명제4), SSS(멍제 8), ASA(명제 26) 합동 정리를 공리처럼 쓰고 있다.
$$\triangle ABC\equiv\triangle DEF$$
